viernes, 12 de diciembre de 2014

TRABAJO DE MATEMÁTICA III -ECONOMÍA Y NEGOCIOS INTERNACIONALES


universidad  peruana austral del Cusco

                                                   asignatura de matemática III

                                                  DOCENTE . Mg. Victor Luis Cruz Mollohanca

integrantes de grupo:

Farfan Choque Juan Carlos
Nina Condori Abel Oswaldo
Ocampo Miranda Roxana
Valenzuela Tapia Sadith


Integral Indefinida 

Definicion. Llamaremos integral indefinida de una funci´on f(x) en un intervalo (a, b)
al conjunto de todas sus funciones primitivas en dicho intervalo. Lo representaremos con
la notaci´on habitual: ∫
f(x) dx. La funci´on f(x) recibe el nombre de integrando.
Las dos propiedades anteriores implican que basta con conocer una primitiva de f(x) en
(a, b), F(x), para conocer la totalidad de ellas, y as´ı tendremos:
∫
f(x) dx = F(x) + C
para cualquier constante real C. (Nota: es habitual no especificar el intervalo en el que
se definen las primitivas, se sobreentiende que siempre es en un abierto en el que F(x)
sea derivable.)
Propiedades. De la definici´on de integral indefinida se deducen de manera trivial las
siguientes propiedades:
•
∫(f(x) + g(x)) dx =∫f(x) dx +∫g(x)dx

• ∀k ∈ R, se verifica: ∫kf(x) dx = k∫f(x) dx
•d
dx (∫f(x) dx)= f(x)

•f′(x) dx = f(x) + C.

Si recordamos la notaci´on habitual de la diferencial de una funci´on: df(x) =
f′(x) dx, es habitual escribir esta propiedad en la forma
:
∫f′(x) dx =∫d(f(x)) = f(x) + C
INTEGRALES VARIAS
 
 
 
                    1.-                                                                   11.- 
                    2.-                                                                       12.- 
                    3.-                                                                    13.- 
                   4.-                                                                      14.- 
                    5.-                                                     15.- 
                    6.-                                                                16.- 
                    7.-                                                               17.- 
                    8.-                                                                    18.- 
                    9.-                                                                     19.- 
                    10.-                                                                
20.-


ANTI DERIVADA 
Concepto:
Dada una función, sabemos como hallar su derivada, este problema
lo estudia el cálculo diferencial. Cuando se conoce la derivada de
una función y se desea conocer la función original, se usa el cálculo
integral.
La antiderivada o primitiva de una funcion f(x) es otra función F(x)+C
donde C es una constante. Si al derivar F(x)+C nos da como respuesta f(x)
Es decir F’(x) = f(x)
A la funcion F(x) se le llama una antiderivada de la una funcion f(x).


Integral indefinida
 es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.

Propiedades de la integral indefinida

1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx



Integrales inmediatas
 son las que salen directamente por la propia definición de integral, es decir, la que se puede resolver de forma más o menos intuitiva pensando en una función que cuando se derive me dé la que está en la integral.
Al igual que hicimos con las derivadas, te pongo una lista de integrales inmediatas, que como puedes comprobar es la contraria de la de las derivadas.

Lista de integrales inmediatas
A continuación se indican algunas técnicas de Integración que nos permitirán encontrar las integrales de una clase muy amplia de funciones.

Todas las técnicas tienen como objetivo reducir la integral buscada a una integral ya conocida o inmediata, como por ejemplo una de las de la tabla ó bien reducirla a una integral más sencilla.




Integración por cambio de variable.
Nos proporciona un proceso que permite reconocer cuándo un integrando es el resultado de una derivada en la que se ha usado la regla de la cadena.

Sea f(x) la función que deseamos integrar, entonces hacemos el siguiente cambio de variable: x = g(t), d(x) = g'(t)dt, con lo que:


Para que la fórmula de cambio de variable tenga posibilidades de éxito, debemos identificar en el integrando a una función u y a u' (su derivada).


Integración por partes.
Este método nos permitirá resolver integrales de funciones que pueden expresarse como un producto de una función por la derivada de otra.

Sean u y v dos funciones continuas, derivables y sus derivadas du y dv son integrables, entonces:

u=f(x), v=g(x), luego du=f'(x)dx, dv=g'(x)dx:




Integración de funciones racionales:
Vamos a integrar funciones racionales (cociente de polinomios), que siguen la forma:

 


a) Si el grado de P(x) es mayor o igual que el grado de Q(x).


En este caso se divide P(x) entre Q(x), pasando la integral a:
Se reduce a calcular la integral de un polinomio c(x) y la integral de una función racional en la cual el numerador tiene grado menor que el denominador (está última integral es la que nos queda por calcular).

A continuación describiremos varios casos de descomposición de fracciones racionales (en las que el polinomio del numerador tiene grado menor que el denominador) como una suma de fracciones parciales, fáciles de integrar.



b) Si el grado de P(x) es menor que el grado de Q(x).

Una fracción simple es cualquier fracción propia de polinomios (el grado del numerador es estrictamente menor que el grado del denominador), cuyo denominador es de la forma (ax + b)n ó (ax2 + bx + c)n


b.1) Q(x) tiene todas sus raíces reales y distintas:
La factorización del polinomio Q(x) es en factores lineales y distintos:

Q(x) = (x-a1)(x-a2)(x-a3)…(x-an), hacemos la siguiente descomposición:
         con A1, ...An constantes reales.

Ejemplo

b.2) Q(x) tiene todas sus raíces reales, pero puede haber repetidas:
La factorización del polinomio Q(x) es en factores lineales no necesariamente distintos, es decir:

Q(x) = (x-a1)m1(x-a2)m2(x-a3)m3…(x-an)mn

De nuevo como en el caso anterior la integración de las fracciones parciales es sencilla y se reduce a calcular integrales de la forma:
las cuales, para n > 1, se resuelven por un sencillo cambio de variable.

Ejemplo


b.3) Q(x) tiene raíces complejas distintas:
Cuando en la factorización del polinomio Q(x) aparecen factores cuadráticos de la forma:

ax2 + bx + c       con      b2 - 4ac < 0

a cada uno de estos factores le corresponde una fracción parcial de la forma:

donde A y B son constantes reales.
Ejemplo

b.4) Q(x) tiene raíces complejas repetidas:
Cuando en la factorización del polinomio Q(x) aparecen factores cuadráticos de la forma:

(ax2 + bx + c)n       con      b2 - 4ac < 0

a cada uno de estos factores le corresponden n fracciones parciales de la forma:

con Ak, Bk constantes reales (k=1, ..n)





ARTIFICIOS DE INTEGRACIÓN 

Concepto de integral definida

La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.
La integral definida de la función entre los extremos del intervalo [a, b] se denota como:

Propiedades de la integral definida

La integral definida cumple las siguientes propiedades:
  • Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
  • Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
  • La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
  • La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
  • Al permutar los límites de una integral, ésta cambia de signo.
  • Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):
  • Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:

Ilustración gráfica del concepto de integral definida.

Función integral

Considerando una función f continua en [a, b] y un valor x Î [a, b], es posible definir una función matemática de la forma:
donde, para no inducir a confusión, se ha modificado la notación de la variable independiente de x a t. Esta función, simbolizada habitualmente por F (x), recibe el nombre de función integral o, también, función área pues cuando f es mayor o igual que cero en [a, b], F (x) nos da el área.

Interpretación geométrica de la función integral o función área.

Teorema fundamental del cálculo integral

La relación entre derivada e integral definida queda establecida definitivamente por medio del denominado teorema fundamental del cálculo integral, que establece que, dada una función f (x), su función integral asociada F (x) cumple necesariamente que:
A partir del teorema fundamental del cálculo integral es posible definir un método para calcular la integral definida de una función f (x) en un intervalo [a, b], denominado regla de Barrow:
  • Se busca primero una función F (x) que verifique que F¿ (x) = f (x).
  • Se calcula el valor de esta función en los extremos del intervalo: F (a) y F (b).
  • El valor de la integral definida entre estos dos puntos vendrá entonces dado por:

Sumatoria


 
La sumatoria o sumatorio se emplea para representar la suma de muchos o infinitos sumandos.
La expresión se lee: "sumatoria de Xi, donde i toma los valores de 1 a n".
La operación sumatoria se expresa con la letra griegra sigma mayúscula Σ.

i es el valor inical llamado límite inferior.
n es el valor final llamado líimite superior.
Si la sumatoria abarca la totalidad de los valores, su expresión se puede simplificar:
Es frecuente el uso del operador sumatoria en Estadística.
La suma de las frecuencias absolutas se puede expresar como:
1. igualdad
2. igualdad
Y la media como:
1.media
2.media

Ejemplo

En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la media.
xifixi · fi
[10, 20)15115
[20, 30)258200
[30,40)3510350
[40, 50)459405
[50, 60558440
[60,70)654260
[70, 80)752150
Σxi = 42Σxi · fi = 1 820
media

Propiedades de las sumatorias

La suma del producto de una constante por una variable, es igual a k veces la sumatoria de la variable.
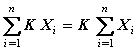
sumatoria
La sumatoria hasta N de una constante, es igual a N veces la constante.
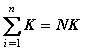
La sumatoria de una suma es igual a la suma de las sumatorias de cada término.
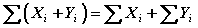
La sumatoria de un producto no es igual al producto de las sumatorias de cada término.
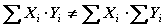
La sumatoria de los cuadrados de los valores de una variable no es igual a la sumatoria de la variable elevado al cuadrado.






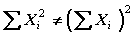
Suma superior. Suma inferior.

Descripción: 
Dado [a,b] un intervalo, y sea P={x₀,x₁,...,xn} una partición del intervalo. Si Mi y mi son los valores máximos y mínimos de f en cada subintervalo d ela partición (xi−1,xi). Definimos
a). Suma superior de f en [a,b] respecto a la partición P a SPsupⁿ=∑ni=1Mi(xi−xi−1)
b). Suma inferior de f en [a,b] respecto a la partición P a sPsup=∑ni=1mi(xi−xi−1)
Descriptores: 
 Integral definida
 Integral
Ejemplo: 
Sea f(x)=2x+3 la función real de variable real definida sobre el intervalo cerrado [0,3] y sea  P={0,0′5,1,2,2′5,3} una partición del intervalo. Calcular la suma supoerior y la suma inferior de f en [0,3] respecto a la partición P
 M0=4;M1=5;M2=7;M3=8;M4=9 . la suma superior de esta función relativa a la partición dada es:
 SPsupⁿ=∑ni=1Mi(xi−xi−1)=4(0′5−0)+5(1−0′5)+7(2−1)+8(2′5−2)+9(3−2′5)=20
 m0=3;m1=4;m2=5;m3=7;m4=8 . la suma inferior de esta función relativa a la partición dada es:



sPsup=∑ni=1mi(xi−xi−1)=3(0′5−0)+4(1−0′5)+5(2−1)+7(2′5−2)+8(3−2′5)=16




INTEGRAL DE RIEMANN
Ahora se va a definir la integral de una función cualquiera definida en un intervalo
[a, b] con la única condición de que esté acotada, es decir, que exista un número M > 0, de forma que la función, en el intervalo [a, b], siempre tome valores entre -M y M.
Volviendo al ejemplo introductorio del tema, f(x) = x, es necesario recordar que para el cálculo del área de un triángulo se tomaron funciones escalonadas g(x) cumpliendo g(x) ð f(x) para cualquier x ð [a, b] y otras funciones escalonadas h(x) tales que f(x) ð h(x) si x ð [a, b]. De todo ello resultaba que:
Integrales. Integral de Riemann. Cálculo integral
En general, para una función f(x) acotada, se toman todas las funciones escalonadas g(x) por defecto, y todas las funciones escalonadas por exceso, es decir, g(x) ð f(x) ð h(x) cuando x ð [a, b]. En estas condiciones, si existe un único número I que cumpla
Integrales. Integral de Riemann. Cálculo integral
para cualesquiera g(x) y h(x) escalonadas, que cumplan g(x) ð f(x) ð h(x) si
x ð [a, b], al número I se le llama integral de f(x) entre a y b.
Integrales. Integral de Riemann. Cálculo integral
y se lee «integral, desde a hasta b, o entre a y b, de f(x),diferencial de x.

significado de la integral definida de una función
ð Si una función positiva f(x), definida en un intervalo [a,b], es integrable (existe su Integrales. Integral de Riemann. Cálculo integral
por la gráfica de la función, el eje de abscisas y las rectas x = a y x = b.
ð Si la función y = f(x) fuese negativa en el intervalo [a, b], la gráfica de la función quedaría por debajo del eje de abscisas.
En este caso, al tomar funciones escalonadas por exceso y por defecto, sus integrales correspondientes serían negativas, y puesto que
Integrales. Integral de Riemann. Cálculo integral
Integrales. Integral de Riemann. Cálculo integral
el área de la región que determina una función negativa es:
Integrales. Integral de Riemann. Cálculo integral
Este hecho no debería llamar la atención si se tiene presente cómo está definida la integral de una función escalonada: la suma de las áreas de los rectángulos que determina con el eje de abscisas, si la función escalonada es positiva y la suma de las áreas de los rectángulos que determina con el eje de abscisas con signo menos, si la función escalonada es negativa.

ð Finalmente, si la gráfica de una función queda parte por encima, y parte por debajo del eje de abscisas, la integral se descompondrá en varios sumandos cuando se quiera calcular el área de la región que delimita con el eje de abscisas en el intervalo [a, b].
Se ve claramente que:
Integrales. Integral de Riemann. Cálculo integral
Integrales. Integral de Riemann. Cálculo integral
Integrales. Integral de Riemann. Cálculo integral
Integrales. Integral de Riemann. Cálculo integral

La definición de integral de Riemann poco ayuda a su cálculo, pues es imposible encontrar todas las funciones escalonadas por defecto y por exceso de otra función dada. Hay, no obstante, criterios que son mucho más útiles de cara a decidir si una función acotada es integrable o no. Uno de ellos se obtiene con el siguiente teorema, cuya demostración se omite por escapar de los objetivos de este libro.







INTEGRALES IMPROPIAS.
Llamaremos integrales impropias a las integrales de funciones sobre intervalos ilimitados, o a las integrales de funciones que no están acotadas en un intervalo.      
Integrales impropias de primera especie. Convergencia. Sea f (x) continua $ \forall$x $ \geq$ a. Si existe $ \lim\limits_{b\rightarrow+\infty}^{}$$ \int_{a}^{b}$f (x) dx, se dice que f tiene una integral impropia convergente en [a, + $ \infty$), y definimos:        
        $ \int_{a}^{+\infty}$f (x) dx = $ \lim\limits_{b\rightarrow+\infty}^{}$$ \int_{a}^{b}$f (x) dx        
Si no existe el límite, diremos que f tiene una integral impropia divergente en [a, + $ \infty$).        
De igual modo, definimos también $ \int_{-\infty}^{b}$f (x) dx = $ \lim\limits_{a\rightarrow-\infty}^{}$$ \int_{a}^{b}$f (x) dx, y        
$ \int_{-\infty}^{+\infty}$f (x) dx = $ \lim\limits_{a\rightarrow-\infty}^{}$$ \int_{a}^{c}$f (x) dx + $ \lim\limits_{b\rightarrow+\infty}^{}$$ \int_{c}^{b}$f (x) dx, si los límites existen.
Ejemplo: Vamos a calcular el área que determina f (x) = $ {\frac{1}{x^{2}}}$ con el eje X, a partir de x = 1.        
$ \int_{1}^{+\infty}$$ {\frac{1}{x^{2}}}$dx = $ \lim\limits_{b\rightarrow+\infty}^{}$$ \int_{1}^{b}$$ {\frac{1}{x^{2}}}$dx = $ \lim\limits_{b\rightarrow+\infty}^{}$$ \left[\vphantom{ \frac{x^{-1}}{-1}}\right.$$ {\frac{x^{-1}}{-1}}$$ \left.\vphantom{ \frac{x^{-1}}{-1}}\right]_{1}^{b}$ = $ \lim\limits_{b\rightarrow+\infty}^{}$$ \left(\vphantom{ \frac{-1}{b}-(-1)}\right.$$ {\frac{-1}{b}}$ - (- 1)$ \left.\vphantom{ \frac{-1}{b}-(-1)}\right)$ = 1 u.a.      
Integrales impropias de segunda especie. Sea f (x) continua en (a, b], y no acotada en a. Si existe $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \int_{a+\delta}^{b}$f (x) dx, definimos:        
        $ \int_{a}^{b}$f (x) dx = $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \int_{a+\delta}^{b}$f (x) dx        
Si el límite no existe, diremos que $ \int_{a}^{b}$f (x) dx es divergente.
Ejemplo: f (x) = ln x continua para x > 0, no está acotada en x = 0. Calculemos el área del recinto que determina con los ejes. La integral indefinida será:        
$ \int_{0}^{1}$ln x dx = $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \int_{0+\delta}^{1}$ln x dx = $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \left[\vphantom{ x\ln x-x}\right.$x ln x - x$ \left.\vphantom{ x\ln x-x}\right]_{\delta}^{1}$ = - 1 - $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \left(\vphantom{ \delta\ln\delta}\right.$$ \delta$ln$ \delta$$ \left.\vphantom{ \delta\ln\delta}\right)$ = - 1.
  El recinto tendrá 1 u.a.
Ejemplo: Calcular el área del recinto que determina f (x) = $ {\frac{1}{(x-1)^{2}}}$ entre x = 0 y x = 2.
La función no está acotada en x = 1.        
S = $ \int_{0}^{1}$$ {\frac{1}{(x-1)^{2}}}$dx + $ \int_{1}^{2}$$ {\frac{1}{(x-1)^{2}}}$dx = $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \int_{0}^{1-\delta}$$ {\frac{1}{(x-1)^{2}}}$dx + $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \int_{1+\delta}^{2}$$ {\frac{1}{(x-1)^{2}}}$dx =        
= $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \left[\vphantom{ -\frac{1}{x-1}}\right.$ - $ {\frac{1}{x-1}}$$ \left.\vphantom{ -\frac{1}{x-1}}\right]_{0}^{1-\delta}$ + $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$$ \left[\vphantom{ -\frac{1}{x-1}}\right.$ - $ {\frac{1}{x-1}}$$ \left.\vphantom{ -\frac{1}{x-1}}\right]_{1+\delta }^{2}$ = $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$($ {\frac{1}{\delta}}$ - 1) + $ \lim\limits_{\delta\rightarrow 0^{+}}^{}$(- 1 + $ {\frac{1}{\delta}}$) = $ \infty$.
 La integral impropia es divergente.    





Integrales impropias con límites de integración infinito"
En los ejercicios 1 a 18, determine si la integral impropia es convergente o divergente, y si es convergente evalúela. Apoye gráficamente la respuesta.


Entre las funciones que se utilizan en economía para hacer modelos de situaciones de mercado se estudian las funciones de oferta y de demanda.
Función de oferta: una empresa que fabrica y vende un determinado producto utiliza esta función para relacionar la cantidad de productos que está dispuesta a ofrecer en el mercado con el precio unitario al que se puede vender esa cantidad. Podemos decir que, en respuesta a distintos precios, existe una cantidad correspondiente de productos que los fabricantes están dispuestos a ofrecer en el mercado en algún período específico.
Cuanto mayor es el precio, mayor será la cantidad de productos que la empresa está dispuesta a ofrecer. Al reducirse el precio, se reduce la cantidad ofrecida. Esto nos permite asegurar que la función de oferta es una función creciente. Si p representa el precio por unidad y q la cantidad ofrecida correspondiente entonces a la ley que relaciona p y q se la denomina función de oferta y a su gráfica se la conoce como gráfica de oferta.
                               
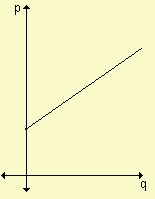
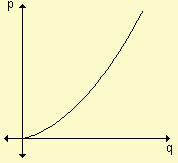
A esta función la simbolizamos p = o(q) donde sabemos que p es el precio unitario y q la cantidad de productos que, a ese precio, se ofrece en el mercado.
Función de demanda: La empresa utiliza esta función para relacionar la cantidad de productos demandada por los consumidores, con el precio unitario al que se puede vender esa cantidad, de acuerdo con la demanda. En general, si el precio aumenta, se produce una disminución de la cantidad demandada del artículo porque no todos los consumidores están dispuestos a pagar un precio mayor por adquirirlo. La demanda disminuye al aumentar el precio por eso esta es una función decreciente como lo observamos en los ejemplos gráficos. Podemos asegurar entonces que para cada precio de un producto existe una cantidad correspondiente de ese producto que los consumidores demandan en determinado período. Si el precio por unidad de un producto está dado por p y la cantidad correspondiente en unidades está dada por q la ley que los relaciona se denomina función de demanda. A su gráfica se la llama gráfica de demanda.
                               
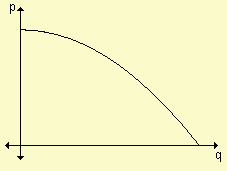
A esta función la simbolizamos p = d(q) donde sabemos que p es el precio unitario y q la cantidad de productos que, a ese precio, se demanda en el mercado.
SUPERAVIT DE CONSUMIDORES Y PRODUCTORES
El mercado determina el precio al que un producto se vende. El punto de intersección de la curva de la demanda y de la curva de la oferta para un producto da el precio de equilibrio. En el precio de equilibrio, los consumidores comprarán la misma cantidad del producto que los fabricantes quieren vender. Sin embargo, algunos consumidores aceptarán gastar más en un artículo que el precio de equilibrio. El total de las diferencias entre el precio de equilibrio del artículo y los mayores precios que todas esas personas aceptan pagar se considera como un ahorro de esas personas y se llama el superávit de los consumidores.
El área bajo la curva de demanda es la cantidad total que los consumidores están dispuestos a pagar por q0 artículos. El área sombreada bajo la recta y = p0 muestra la cantidad total que los consumidores realmente gastarán en el precio p0 de equilibrio. El área entre la curva y la recta representa el superávit de los consumidores.
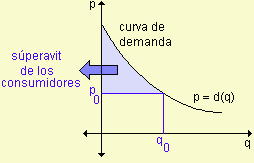
El superávit de los consumidores está dado por el área entre las curvas p = d(q) y p = p0 entonces su valor puede encontrarse con una integral definida de esta forma:
 donde d(q) es una función demanda con precio de equilibrio p0 y demanda de equilibrio q0.

Problema


La curva de demanda está dada por la ley d(x) = 50 - 0,06x2. Encuentre el superávit o ganancia de los consumidores si el nivel de venta asciende a veinte unidades.
Como la cantidad de unidades es 20, su precio asciende a p = d(20) = 50 - 0,06 202 = 26.
Resolviendo la integral, la ganancia de los consumidores resulta:
=  =  = 320
La ganancia de los consumidores asciende a $ 320 si el nivel de venta asciende a veinte unidades.
De la misma manera si algunos fabricantes estuviesen dispuestos a proporcionar un producto a un menor precio que el precio p0 de equilibrio, el total de las diferencias entre el precio de equilibrio y los precios más bajos a los que los fabricantes venderían el producto se considera como una entrada adicional para los fabricantes y se llama el superávit de los productores.
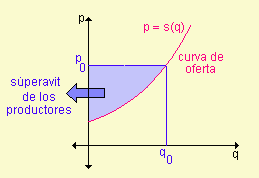
El área total bajo la curva de oferta entre q = 0 y q = q0 es la cantidad mínima total que los fabricantes están dispuestos a obtener por la venta de q0 artículos. El área total bajo la recta p =p0 es la cantidad realmente obtenida. La diferencia entre esas dos áreas, el superávit de los productores, también está dada por una integral definida.
Si s(q) es una función de oferta con precio p0 de equilibrio y oferta q0 de equilibrio, entonces superávit de los productores =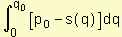 

Problema


Se conoce que la curva de la oferta para un producto es s(x) = 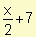. Encuentre la ganancia de los productores si la producción asciende a diez artículos.
Si la producción asciende a 10 artículos el precio es s(10) = 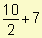= 12 pesos.
La ganancia o superávit de los productores se calculo resolviendo:
 = = 
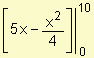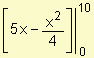Ganancia de las productores = = 25
La ganancia de los productores asciende a $25 si la producción es de diez artículos.

Problema


Calcule el exceso de oferta y el exceso de demanda para las curvas de demanda y oferta dadas.
Función de demanda: p1 (q) = 1000 - 0,4 q2. Función de oferta: p2 (q) = 42q
El exceso de oferta y el de demanda están representados por las áreas que muestra la gráfica:
La oferta coincide con la demanda en (q0, p0) , es decir,:
p1 (q) = p2 (q) Þ 1000 - 0,4q2 = 42q Þ - 0,4q2 - 42q + 1000 = 0 Þ
q1 = - 125 Ù q2 = 20
Como los valores de las abscisas corresponde a número de artículos ofrecidos o demandados, q0 = 20 y, por lo tanto, p0 = 840.
El excedente de demanda o superavit de los consumidores es la región comprendida entre p1 (q)  y  la recta   p = 840, entre 0 y 20, o sea,:
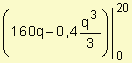 = =  = 2133,33
El excedente de demanda asciende a $2133,33
El excedente de oferta es la región comprendida entre las rectas p = 840 y p = 42q entre 0 y 20, o sea:
 = = (840.20 - 21.202) = 8400
El superavit de oferta alcanza $8400.

ANÁLISIS MARGINAL
La derivada y, en consecuencia la integral, tienen aplicaciones en administración y economía en la construcción de las tasas marginales.
Es importante para los economistas este trabajo con el análisis marginal porque permite calcular el punto de maximización de utilidades.
En el análisis marginal se examinan los efectos incrementales en la rentabilidad. Si una firma está produciendo determinado número de unidades al año, el análisis marginal se ocupa del efecto que se refleja en la utilidad si se produce y se vende una unidad más.
Para que este método pueda aplicarse a la maximización de utilidades se deben cumplir las siguientes condiciones:
    • Deberá ser posible identificar por separado las funciones de ingreso total y de costo total.
    • Las funciones de ingreso y costo deben formularse en términos del nivel de producción o del número de unidades producidas y vendidas.
    Damos algunas definiciones importantes para nuestro trabajo:
    Costo marginal: es el costo adicional que se obtiene al producir y vender una unidad más de un producto o servicio.
    También se puede definir como el valor límite del costo promedio por artículo extra cuando este número de artículos extra tiende a cero.
    Podemos pensar el costo marginal como el costo promedio por artículo extra cuando se efectúa un cambio muy pequeño en la cantidad producida.
    Debemos tener en cuenta que si c(x) es la función costo, el costo promedio de producir x artículos es el costo total dividido por el número de artículos producidos.
    Costo promedio por artículo =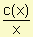 
    Costo marginal =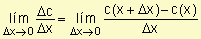 
    Costo marginal = c'(x) =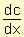 
    El costo marginal mide la tasa con que el costo se incrementa con respecto al incremento de la cantidad producida.
    Ingreso marginal: es el ingreso adicional que se consigue al vender una unidad más de un producto o servicio.
    Para una función de ingreso total r(x), la derivada r’(x) representa la tasa instantánea de cambio en el ingreso total con un cambio del número de unidades vendidas. Podemos decir que el ingreso marginal representa las entradas adicionales de una empresa por artículo adicional vendido cuando ocurre un incremento muy pequeño en el número de artículos vendidos. Representa la tasa con que crece el ingreso con respecto al incremento del volumen de ventas.
    Utilidad marginal que obtiene una empresa está dada por la diferencia entre sus ingresos y sus costos. Si la función de ingreso es r(x) cuando se venden x artículos y si la función de costo es c(x) al producirse esos mismos artículos, la utilidad  p(x)  obtenida por producir y vender  x  artículos está dada por p(x) = r(x) – c(x).
    La derivada p’(x) se denomina utilidad marginal y representa la utilidad por artículo si la producción sufre un pequeño incremento.
    Resuelva los siguientes problemas y verifique las respuestas.

    Problema
    Una función de costo marginal está definida por c'(x) = 3x2 + 8x + 4 y el costo fijo es de $6. Determine la función costo total correspondiente.
    Respuesta: c(x) =  x3 + 4x2 +4x + 6
      
    Problema


    Para un artículo particular, la función de ingreso marginal es i'(x) = 15 - 4x. Si x unidades son demandadas cuando el precio por unidad es de p pesos:
    a) Determine la función ingreso total.
    b) Determine la ecuación de demanda.
    Respuestas: a) i(x) =  15x - 2x2      b) p(x) =  15 - 2x

    Analice los problemas resueltos a continuación.

    Problema
    Suponemos que durante los primeros cinco años que un producto se puso a la venta en el mercado la función f(x) describe la razón de ventas cuando pasaron x años desde que el producto se presentó en el mercado por primera vez. Se sabe que 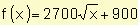 si 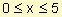. Calcule las ventas totales durante los primeros cuatro años.
    Debemos plantear Venta total =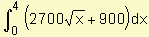 
    Venta total = 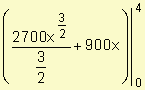= = 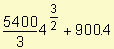18000
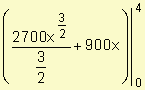    Las ventas totales durante los primeros cuatro años ascienden a 18000 unidades.

    Problema


    Se espera que la compra de una nueva máquina genere un ahorro en los costos de operación. Cuando la máquina tenga x años de uso la razón de ahorro sea de f(x) pesos al año donde f(x) = 1000 + 5000x.
    a) ¿Cuánto se ahorra en costos de operación durante los primeros seis años?
    b) Si la máquina se compró a $ 67500 ¿cuánto tiempo tardará la máquina en pagarse por sí sola?
    a) Para conseguir el ahorro durante los primeros seis años calculamos
    Al cabo de seis años el ahorro asciende de $ 96000
    b) Dado que el precio de compra es de $ 67500, el número de años de uso que se requieren para que la máquina se pague sola es n, entonces
    1000n + 2500 n2 = 67500 Þ 2500 n2 + 1000n - 67500 = 0
    5 n2 + 2n - 135 = 0
    Hallamos los valores de n aplicando la resolvente  y resulta  n1 = -5,4  (imposible para nuestro problema) y además n2 = 5.
    Se tardarán 5 años para que la máquina se pague sola.

    Sólo se enuncian algunas de las muchas aplicaciones de la integral definida a la resolución de problemas, sólo se pretende motivar para una indagación e investigación más profunda.













    Publicado por en No hay comentarios:
    Etiquetas:
    Suscribirse a: Entradas (Atom)